robotics section 3 matlab practice

本练习主要讨论平面3自由度、3R机器人的DH坐标参数和正向(位姿)运动学变换方程(见图3-6和图3-7)。已知下列固定长度参数:\(L_1=4\),\(L_2=3\)和\(L_3=2\)(米)。

a

题目

求D-H参数。

解答

clear;clc;
syms theta1 theta2 theta3 l1 l2 l3%符号函数，真的好用
L(1) = Link([theta1 0 0 0],'modified');
L(2) = Link([theta2 0 l1 0],'modified');
L(3) = Link([theta3 0 l2 0],'modified');
Three_Link = SerialLink(L,'name','threelink');
Three_Link.display;

结果

result_a

b

题目

推导相邻的齐次变换矩阵\(^{i-1}_{i}T\)，它们是关节角度变量\(\theta_i\)(i=1,2,3)的函数。用试探法推导常量矩阵\(^3_HT\)。这里，{H}的原点在夹爪手指的中心，{H}的姿态与{3}的姿态相同。

解答

clc;clear;
syms theta1 theta2 theta3 theta4 l1 l2 l3
%齐次变换矩阵
syms alphai_1 ai_1 di thetai
i_1iT=[cos(thetai) -sin(thetai) 0 ai_1
    sin(thetai)*cos(alphai_1) cos(thetai)*cos(alphai_1) -sin(alphai_1) -sin(alphai_1)*di
    sin(thetai)*sin(alphai_1) cos(thetai)*sin(alphai_1) cos(alphai_1) cos(alphai_1)*di
    0 0 0 1];
%R = subs(S, old, new) 利用new的值代替符号表达式中old的值
T01=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 0 0 theta1])
T12=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 l1 0 theta2])
T23=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 l2 0 theta3])
T3H=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 l3 0 0])

结果

result_b

c

题目

用MATLAB符号法求正向运动学解\(^0_3T\)和\(^0_HT\)(\(\theta _i\)的函数)。用s=sin(\(\theta\)),c=cos(\(\theta\))等简写你的结果。由于\(Z_i\)轴相互平行，因此可以用二角和公式将(\(\theta_1 + \theta_2 + \theta_3\))简写。用MATLAB计算正向运动学解(\(^0_3T\)和\(^0_HT\))。输入参数为:
i) \(\theta_1\)=0°,\(\theta_2\)=0°,\(\theta_3\)=0°;
ii) \(\theta_1\)=10°,\(\theta_2\)=20°,\(\theta_3\)=30°;
iii) \(\theta_1\)=90°,\(\theta_2\)=90°,\(\theta_3\)=90°;
对于这三种情况，可以利用操作臂位形简图校核结果，用试探法推导正向运动学变换(参考由旋转矩阵和位置矢量定义\(^0_HT\)的方法)。简图中包括坐标系{H}，{3}和{0}。

解答

clc;clear;
syms theta1 theta2 theta3 theta4 l1 l2 l3
%齐次变换矩阵
syms alphai_1 ai_1 di thetai
i_1iT=[cos(thetai) -sin(thetai) 0 ai_1
    sin(thetai)*cos(alphai_1) cos(thetai)*cos(alphai_1) -sin(alphai_1) -sin(alphai_1)*di
    sin(thetai)*sin(alphai_1) cos(thetai)*sin(alphai_1) cos(alphai_1) cos(alphai_1)*di
    0 0 0 1];
%R = subs(S, old, new) 利用new的值代替符号表达式中old的值
T01=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 0 0 theta1]);
T12=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 l1 0 theta2]);
T23=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 l2 0 theta3]);
T3H=subs(i_1iT,[alphai_1 ai_1 di thetai],[0 l3 0 0]);
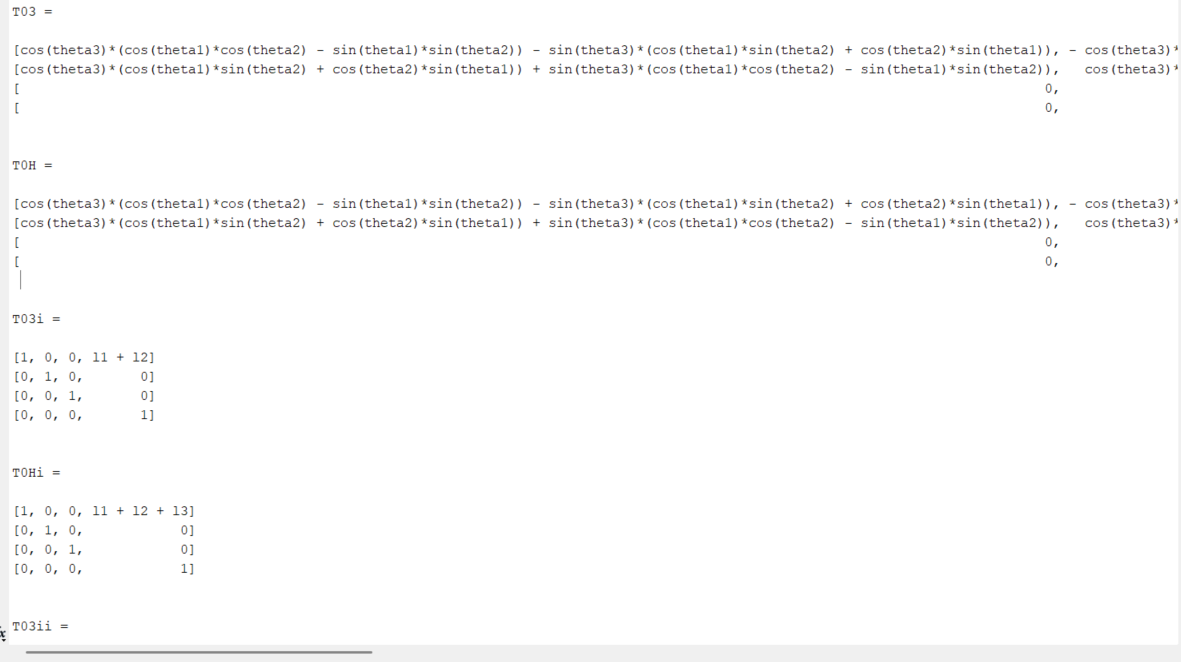
T03=T01*T12*T23
T0H=T01*T12*T23*T3H
T03i=subs(T03,[theta1 theta2 theta3],[0 0 0])
T0Hi=subs(T0H,[theta1 theta2 theta3],[0 0 0])
T03ii=subs(T03,[theta1 theta2 theta3],[10 20 30])
T0Hii=subs(T0H,[theta1 theta2 theta3],[10 20 30])
T03iii=subs(T03,[theta1 theta2 theta3],[10 20 30])
T0Hiii=subs(T0H,[theta1 theta2 theta3],[10 20 30])

结果

d

题目

用Corke MATLAB Robotics工具箱检验计算结果。试用函数link()，robot()和fkine()。

解答

syms theta1 theta2 theta3 L1 L2 L3
L(1) = Link([theta1 0  0 0 0],'modified');
L(2) = Link([theta2 0  4 0 0],'modified');
L(3) = Link([theta3 0  3 0 0],'modified');
L(4) = Link([0      0  2 0 1],'modified');
Three_Link = SerialLink(L,'name','threelink');
%用户输入均为角度
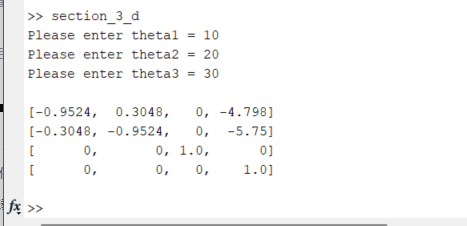
theta1 = input ('Please enter theta1 = ');
theta2 = input ('Please enter theta2 = ');
theta3 = input ('Please enter theta3 = ');
%只要有一个输入为空，就结束程序
empty = isempty(theta1)+isempty(theta2)+isempty(theta3);
if empty>0
    fprintf('Error!');
else     
    digits(4);%设置只保留小数点后4位
    T = Three_Link.fkine([theta1,theta2,theta3,0]);%此时为分数
    A = vpa(T)%变换为小数输出
end

结果

result_d