multi agent replication

论文《Event-triggered Design for Optimal Output Consensus of High-order Multi-agent Systems》复现

1. 论文信息

论文标题: Event-triggered Design for Optimal Output Consensus of High-order Multi-agent Systems
论文链接: Event-triggered Design for Optimal Output Consensus of High-order Multi-agent Systems
作者: Yutao Tang, Huaihui Liu, Ruonan Li, Kui Zhu
Abstract: This paper studies the optimal output consensus problem for a group of heterogeneous linear multi-agent systems. Different from existing results, we aim at effective controllers for these high-order agents under both event-triggered control and event-triggered communication settings. We conduct an embedded design for the problem and constructively propose a multi-rate event-triggered controller with a set of applicable parameters. The proposed event-triggered rules are shown to be free of Zeno behaviors and can achieve the optimal output consensus goal for these high-order agents. A simulation example is given to verify the efficacy of our designs.

代码复现

依赖Eigen库进行矩阵计算, clion编译运行.

绘图使用matplotlib, 编译器为pycharm.

1. 代码结构

agent.h # agent类的头文件
agent.cpp # 对单个agent的定义, 核心代码
test.cpp # 测试函数, 用于测试单个agent的运行
main.cpp # 主函数, 对论文仿真示例的实现

核心部分就是UpdateController, UpdateSignalGenerator, UpdateDynamics三个函数. UpdateSignalGenerator实现upper lawer, 核心部分就是UpdateController实现lower lawer. 首先调用ShouldTrigger函数判断是否满足ETC条件, 如果满足, 则更新输入. UpdateDynamics三个函数实现agent的动力学更新.

状态的更新采用Runge-Kutta方法, 实现方法如下:

auto rk4 = [&](const Eigen::VectorXd& x_in) -> Eigen::VectorXd {
        return A_ * x_in + B_ * u_;
};
Eigen::VectorXd k1 = rk4(x_);
Eigen::VectorXd k2 = rk4(x_ + 0.5 * dt * k1);
Eigen::VectorXd k3 = rk4(x_ + 0.5 * dt * k2);
Eigen::VectorXd k4 = rk4(x_ + dt * k3);
x_ = x_ + (dt / 6) * (k1 + 2 * k2 + 2 * k3 + k4);

plot目录下为python绘图代码.

1
2
3

plot/plot.py # 绘图代码
plot/z.png # 仿真结果
test.py # 测试代码, 可以忽略

2. 仿真结果

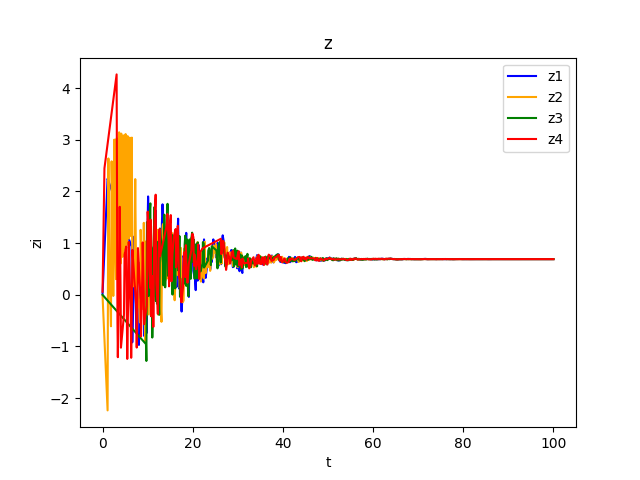
效果不好, 但是可以看出, 一致性是达到了的, 收敛到0.5附近.

3. 期间遇到的问题

3.1 Event-triggered-control(ETC)设计死锁

起初在实现ETC逻辑时, 采用的方法是先判断是否满足ETC条件, 再判断是否需要更新输入. 这种情况会导致agent的状态不更新, 造成死锁. 也就是说, ETC条件是永远不满足的, 因为依赖agent的状态更新. 而agent状态更新的前提是ETC条件满足. 解决方法是, 引入state_new变量, 先更新状态, 再判断event-trigger条件, 如果满足条件, 则更新状态. 这样就可以避免死锁问题.

代码中的实现如下:

u_new_ = K1_ * x_ + K2_ * z_;
if(ShouldTriggerControl(t)) {
    u_ = u_new_;
    u_hat_ = u_;
    last_control_time_ = t;
}

然而, 笔者在完成此逻辑后, 不由产生了一个疑问, ETC的设计是为了减少资源消耗, 但是如果每次都更新状态, 那么不就失去了ETC的意义吗? 后面找了找资料, 仔细想了想, 大概可以这样理解: ETC节省的是执行, 而不是观测和预测. 观测不可避免, 获取系统状态是必需的, 但是执行是可以避免的. ETC的设计主要是为了减少执行的频率, 减少通信/执行开销.

3.2 z的更新问题

在实现z更新的逻辑时, ShouldTriggerCommunication是写错了的, 所以跑出来的结果很奇怪. 当时是判断ETC条件满足后, 更新z. 实际上应该是更新z_dot才对, 也就是z的导数. 而z的更新是整个过程都要进行的. z的更新也是采用了Runge-Kutta方法. 这个问题已经修复了.

auto [k1_z, k1_v] = rk4(z_, v_);
auto [k2_z, k2_v] = rk4(z_ + 0.5 * dt * k1_z, v_ + 0.5 * dt * k1_v);
auto [k3_z, k3_v] = rk4(z_ + 0.5 * dt * k2_z, v_ + 0.5 * dt * k2_v);
auto [k4_z, k4_v] = rk4(z_ + dt * k3_z, v_ + dt * k3_v);
z_dot_new_ = (1.0 / 6) * (k1_z + 2 * k2_z + 2 * k3_z + k4_z);
v_dot_new_ = (1.0 / 6) * (k1_v + 2 * k2_v + 2 * k3_v + k4_v);
if(ShouldTriggerCommunication(t)) {
    z_dot_ = z_dot_new_;
    v_dot_ = v_dot_new_;
    z_hat_ = z_;
    v_hat_ = v_;
    last_comm_time_ = t;
}
z_ += z_dot_ * dt;
v_ += v_dot_ * dt;

还有就是注意1.0/6的写法, 不能直接写成1/6, 否则会变成0~

3.3 参数疑问

最后得到的结果很不好, 可能是参数设置的问题, 更有可能是笔者对论文理解的不够深入, 所以部分逻辑实现错误.

Agent-3

仿真结果得到z是满足一致性要求的, 但是agent-3的状态输出y却没办法收敛到z3. 暂时没有找到原因.

理论分析

1. 理论基础

对于多智能体系统, 考虑高阶线性系统:
$$ \[\begin{aligned} \dot{x}_i(t) &= A_ix_i(t) + B_iu_i(t), \\ y_i(t) &= C_ix_i(t), \\ \end{aligned}\]

$$ 每个智能体具有不同的动态特性(异构).

考虑最优一致性问题, 目标是设计控制器使得所有智能体的输出一致, 设计分布式控制器使得:
\[ \begin{aligned} \lim_{t \to \infty} | y_i(t) - y_j(t) | \to 0,\\ \lim_{t \to \infty} y_i(t) = y^* \\ \end{aligned} \] 上面第一个式子保证i-th智能体和其邻居j-th智能体的输出一致, 第二个式子保证所有智能体的输出一致. 其中$y^*$是所有智能体的输出一致性目标, 也是下列最优控制问题的解:
\[ \begin{aligned} y^* = \arg \min_{s \in R} \sum_{i=1}^N f_i(s) \\ \end{aligned} \] 其中函数$f_i(s)$是每个智能体的局部目标函数, 由每个智能体的状态输出决定.

总的来说, 论文的目标是设计一个分布式控制器, 使得所有智能体的输出一致, 并且最小化每个智能体的局部目标函数.

2. 信号生成器设计

我们期望每个agent i生成一个状态$y_i$, 使得所有的$y_i(t) \to y^*$, 其中:
\[ \begin{aligned} y^* = \arg \min_{s \in R} \sum_{i=1}^N f_i(s) \\ \end{aligned} \]

梯度下降

对优化问题:
\[ \min_{s \in R} \sum_{i=1}^N f_i(s) \] 经典梯度下降为:
\[ s_{k+1} = s_k - \alpha \nabla f(s_k) \] 可以写作:
\[ \dot{z} = -\alpha \sum_{i=1}^N \nabla f_i(z) \] 分布式控制下, 每个agent i都可以得到局部目标函数$f_i$, 于是设计如下的控制器:
\[ \dot{z}_i = -\alpha \nabla f_i(z_i) + \beta \sum_{j = 1}^{N} a_{ij} (z_i - z_j) \] 上式是论文中的写法, 引入了$a_{ij}$, 也就是邻接矩阵, 使得每个agent i只和其邻居进行通信. 当agent i和j相邻时, $a_{ij} = 1$, 否则$a_{ij} = 0$. 等价于:
\[ \dot{z}_i = -\alpha \nabla f_i(z_i) + \beta \sum_{j \in N_i} (z_i - z_j) \] 其中$N_i$是agent i的邻居集合.

上式可以看作是一个分布式的梯度下降算法, 其中第一项是agent i的局部目标函数的梯度, 驱动$z_i$向$f_i$的最小点收敛, 以满足局部最优目标, 第二项是agent i和其邻居之间的差异, 驱动$z_i$向邻居靠拢, 体现一致性的满足. 通过调整$\alpha$和$\beta$的值, 可以控制每个agent的收敛速度和一致性.

辅助变量

上述算法对于高阶系统或复杂网络不够稳定, 在事件触发控制环境下收敛精度不高或速度慢. 于是引入辅助变量$v_i$增加一个"动量项", 使得每个agent i的控制器为:
\[ \begin{aligned} \dot{z}_i &= -\alpha \nabla f_i(z_i) + \beta \sum_{j \in N_i} (z_i - z_j) + \sum_{j \in N_i} (v_i - v_j), \\ \dot{v}_i &= \alpha \beta \sum_{j \in N_i} (z_i - z_j)\\ \end{aligned} \] 可以理解为, $v_i$是一个积分项, 类似于PID控制中的积分项, 用于增加系统的稳定性:
\[ \dot{v}_i = \alpha \beta \sum_{j \in N_i} (z_i - z_j) \] 得到 \[ v_i = \alpha \beta \int_0^t \sum_{j \in N_i} (z_i - z_j) dt \] $v_i - v_j$可以理解为历史中一致性误差反馈, 根据历史中邻居agent作用的大小来判断当前是要"缓一缓"还是要"加速", 从而更柔和和稳定, 快速达到一致性.

github仓库:multi_agent
博客:multi-agent-replication

分布式控制

#论文复现

multi agent replication

https://symcreg.github.io/2025/04/12/multi-agent-replication/

作者

sam

发布于

2025年4月12日

许可协议

robotics section 3 matlab practice 上一篇

robotics section 2 practice 1 下一篇