robotics section 2 practice 1

a

题目

用Z-Y-X(\(\alpha\)-\(\beta\)-\(\gamma\))欧拉角表示法，写出MATLAB程序，当用户输入欧拉角\(\alpha\)-\(\beta\)-\(\gamma\)时，计算旋转矩阵\(^A_BR\)。

解答

%%ZYX欧拉角转旋转矩阵
%输入角度
R_z=input('Rotate around the z-axis in alpha =');
R_y=input('Rotate around the y-axis in beta =');
R_x=input('Rotate around the x-axis in gamma =');
%只要有一个输入为空，输出警告
if isempty(R_z)+isempty(R_y)+isempty(R_x)>0
    fprintf('Error!');
else
    R=rotz(R_z)*roty(R_y)*rotx(R_x);%ZYX
end

结果

b

题目

编写一个MATLAB程序。当输入旋转矩阵\(^A_BR\)时，计算出欧拉角\(\alpha\)-\(\beta\)-\(\gamma\)(反解问题)。计算两个可能的解。证明a)中两种情况的反解。使用循环方法检查你的结果是否正确(即将a)中的欧拉角输入到程序a;将得到的旋转矩阵\(^A_BR\)输入到程序b;你将得到两组解答:一组应当是用户原来的输入值，而另一组可用a)中的程序反复验证。

解答

%% 旋转矩阵转 ZYX 欧拉角
% 输入旋转矩阵
R_11 = input('R_11 = ');
R_12 = input('R_12 = ');
R_13 = input('R_13 = ');
R_21 = input('R_21 = ');
R_22 = input('R_22 = ');
R_23 = input('R_23 = ');
R_31 = input('R_31 = ');
R_32 = input('R_32 = ');
R_33 = input('R_33 = ');

if isempty(R_11) || isempty(R_12) || isempty(R_13) || ...
   isempty(R_21) || isempty(R_22) || isempty(R_23) || ...
   isempty(R_31) || isempty(R_32) || isempty(R_33)
    fprintf('Error! Missing input.\n');
else
    R = [R_11, R_12, R_13;
         R_21, R_22, R_23;
         R_31, R_32, R_33];
    
    % 判断是否接近gimbal lock
    if abs(R(3,1)) < 1
        pitch = -asin(R(3,1));
        roll = atan2(R(3,2)/cos(pitch), R(3,3)/cos(pitch));
        yaw  = atan2(R(2,1)/cos(pitch), R(1,1)/cos(pitch));
    else
        % pitch = ±pi/2，Gimbal lock 情况
        pitch = pi/2 * sign(-R(3,1));
        roll = 0;
        yaw = atan2(-R(1,2), R(2,2));
    end

    % 转为角度
    roll_deg = rad2deg(roll);
    pitch_deg = rad2deg(pitch);
    yaw_deg = rad2deg(yaw);

    fprintf('ZYX欧拉角（角度制）:\n');
    fprintf('Roll  = %.4f°\n', roll_deg);
    fprintf('Pitch = %.4f°\n', pitch_deg);
    fprintf('Yaw   = %.4f°\n', yaw_deg);
end

结果

result_b

c

题目

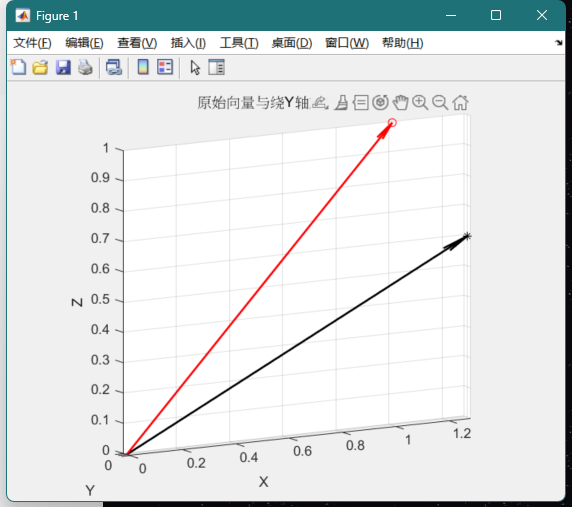
仅简单地绕Y轴旋转\(\beta\)角。已知\(\beta\)=20°和\(^BP=\{1, 0, 1\}^T\)，计算\(^Ap\);用草图验证结果是否正确。

解答

% 定义绕 Y 轴旋转的旋转矩阵（单位为度）
theta = deg2rad(20);  % 将 20 度转为弧度
RAB = [ cos(theta), 0, sin(theta);
               0, 1,         0;
       -sin(theta), 0, cos(theta)];

% 定义向量 PB
PB = [1; 0; 1];

% 原始向量起点处画点
plot3(1, 0, 1, 'o', 'color', 'red');
hold on;

% 绘制原始向量 PB 的箭头
quiver3(0, 0, 0, PB(1), PB(2), PB(3), 1, 'r', 'LineWidth', 1.5);
hold on;

% 旋转后的向量 PA
PA = RAB * PB;

% 绘制旋转后向量 PA 的箭头
plot3(PA(1), PA(2), PA(3), '*', 'color', 'black');
quiver3(0, 0, 0, PA(1), PA(2), PA(3), 1, 'k', 'LineWidth', 1.5);

% 定义坐标轴范围
xlim([-1, 1.5]);
ylim([-1, 1.5]);
zlim([-1, 1.5]);

% 添加坐标轴标签和网格
xlabel('X');
ylabel('Y');
zlabel('Z');
grid on;
axis equal;
view(3);  % 三维视角
title('原始向量与绕Y轴旋转后的向量');
legend('PB', 'PA');

结果

result_c